ELECTRICAL BASICS – Part 1 – DC
ELECTRICAL BASICS – Part 1 – DC
The following was written for electricians and would-be electricians alike, in an effort to introduce and explain the basic concepts of electricity in the sequence in which these concepts were discovered and developed historically. It was intended to assist in the training of electricians.
Section 1 – BASIC DEFINITIONS – Work and Power
Section 2 – BASIC DEFINITIONS – Charge and Current
Section 3 – BASIC DEFINITIONS – Voltage
Section 4 – BASIC DEFINITIONS – Resistance
Section 5 – OHM’S LAW
Section 6 – APPLICATION OF OHM’S LAW
Section 7 – CIRCUITS
Section 8 – VOLTAGE DROP
Section 9 – POWER
Section 10 – CHARGING A BATTERY
Section 11 – POWER LOSS
Section 12 – EFFICIENCY
Section 13 – TEMPERATURE AND RESISTANCE
Section 14 – PARALLEL CIRCUITS
Section 1 – BASIC DEFINITIONS – Work and Power
Unit: A specific amount or magnitude of some quantity such as volume, length, weight, etc. which is established by definition.
The Dollar is the basic unit of currency in the USA. Other units of currency exist such as the Penny, the Nickel, and the Dime. These units of currency are defined in terms of the more basic unit of currency, the Dollar.
Similarly, a “foot” is a unit of length and a “second” is a unit of time.
When measuring any quantity the “unit” of measurement must be understood or defined if communication of data is to be possible. Stating that an object is 3 long communicates nothing. Stating that an object is 3 inches long says it all.
Work (Common usage): Any activity that requires the exertion of muscular or mental effort.
Work (Scientific usage): When a force exerted on a body causes a displacement or change of location of that body in the direction of that force, work is done. The amount of work done is equal to the amount of force applied times the distance moved in the direction of that force.
The first definition corresponds to the common usage of the term ‘work’. For instance, if you were to hold one pound of weight stationary in the air, out horizontally at arms length, you would eventually grow tired and perhaps say that you had done considerable work by having supported that weight.
But what if the upward force of one pound needed to support this weight at a constant elevation were supplied by a table or other stationary platform? Would any work have been done? According to definition 2 above, the answer is no. The table would not have done any work. The weight and the table would both have just sat there, motionless, doing nothing.
Definition 2 specifies that work would only be done when the applied force causes a displacement in the direction of the applied force. Examples would include a stretching a spring, lifting a weight, compressing some gaseous material, or pumping water, etc.
This is not to say that no work was done within the body of the person doing the holding. The heart would have done more work pumping blood through the body to supply the increased needs of the muscles involved, breathing would have increased resulting in more work being done due to the increased forces and motion of the lungs, etc. Other factors also contribute to the tiredness or fatigue one might experience from simply having supported such a weight.
Energy: The capacity or ability to do work.
Energy comes in many forms. It can be stored in many forms. For instance, the work an elevated object can do is equal to the work required to lift that object to that elevation. Its ability to do work is in the form of potential energy when elevated. If it were allowed to fall freely from its height, as it fell, its potential energy would begin to change to kinetic energy, more commonly known as motion energy or the energy of motion. Its velocity would increase as it fell, and so its kinetic energy would become greater. If this object now hit the ground, its kinetic energy would be transformed into other forms of energy, which would include amongst others mostly sound and heat. But regardless of the types or forms of energy resulting from this collision, all are capable of causing displacement by the application of force. Heat can cause displacement by expansion and sound can cause displacement by vibration. This is by definition work!
Joule: A unit of energy equal to the amount of energy (work) required to lift one pound (weight) to an elevation of 0.7376 feet (8.85 inches).
The joule was not originally defined in terms of the English units of inches and pounds. This is true of most of the units used in electrical measurement. The system of units from which the joule was derived is known as the “MKS” system (Meters, Kilograms, and Seconds). In the “MKS” system, the unit of force is known as a newton (1 newton = 0.2247 pounds). One joule is defined as the amount of work required to lift a weight of 1 newton a distance of 1 meter.
Named in honor of Sir James P. Joule (1818-1889), an English scientist who did extensive research into the relationships of electrical, thermal, and mechanical energy circa 1841. (Abbreviated J.)
Power: The rate at which work is being done (energy expended per unit of time). A motor is given a power rating to indicate the rate at which the motor should be able to do work – so much energy output per second.
Watt: A unit of power equal to one joule of energy supplied each second. Lifting one pound to an 8.85 inch higher elevation every second is equivalent to one watt of power. (Abbreviated W.)
Named in honor of James Watt (1736-1819), a Scottish inventor and engineer noted especially for his work on the steam engine.
Horsepower: A unit of power equal to 745.6 Watts. (Abbreviated hp.)
Since 1 watt supplies enough energy in one second to lift one pound of weight to a height of 8.85 inches, one horsepower would be enough energy in one second to lift 745.6 pounds to a height of 8.85 inches.
Horsepower is a very common term in many countries. However, motors from many countries (Germany for instance) are often marked with the motor power in watts rather than horsepower (745.6 watts = 1 hp).
The “Efficiency” rating of a device or machine tells what portion of the total input power to that device or machine will be available as output power. Motors are not 100% efficient. That is, more power must be supplied to a motor than will be available from the output shaft of the motor. Where does the excess power go? It is mostly lost in the form of heat. Some power would also be lost in the form of sound and other mechanical vibration.
It can be demonstrated that the rate at which energy is being lost in all of the various possible forms, added to the rate at which energy is flowing out through the output shaft, is equal to the rate at which energy is being supplied to the motor. This is often phrased as “Power in equals power out,” and is an example of what is meant by “conservation of energy”.
The average efficiency of motors varies with the size of the motor and the size of the load being driven. Peak efficiency is often reached at or near full load. Larger motors are generally more efficient than smaller motors. Below are some typical motor efficiencies:
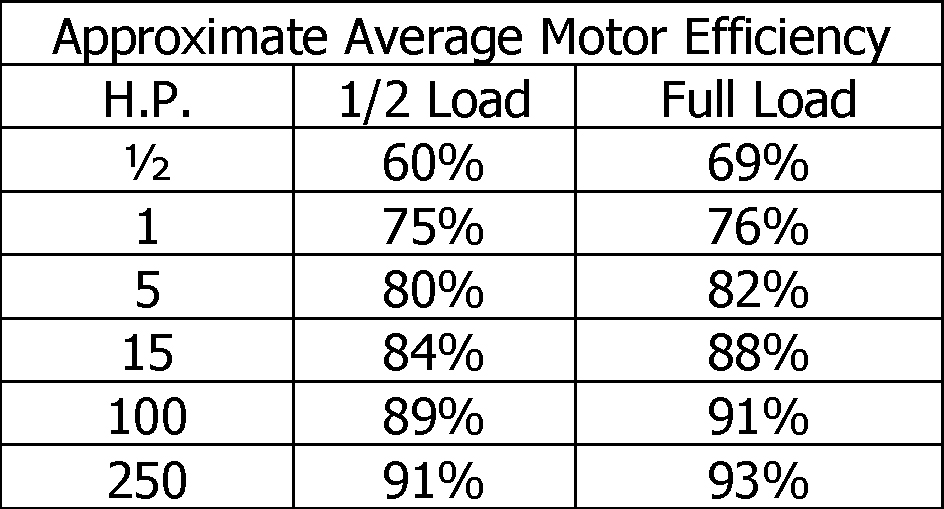
The efficiency tells the percentage of the input power that will be available as output power. Thus according to the above table, an average 1 Horsepower motor would only convert approximately 75% of the incoming power to rotational power (output). Thus, in order to have 1 full horsepower (745.6 watts) of output from an average 1 horsepower motor, an input power of 994.1 watts would be required.
.75 x 994.1 watts = 745.6 watts
Watt-Hour: A unit of energy equal to the total amount of energy that would be delivered in 1 hour of time if the rate of energy flow was 1 watt (one Joule per second). The number of watts times the number of hours equals the number of watt-hours. (Abbreviated Wh.)
One watt-hour equals 3600 Joules of energy. This is the amount of work required to lift 3600 pounds of weight to a height of 8.85 inches or 36 pounds to a height of 885 inches (73.75 feet).
Kilo: A prefix meaning 1,000. (Abbreviated k.)
Kilowatt-hour: A unit of energy equal to 1,000 watt-hours. (Abbreviated kWh.)
Mega: A prefix meaning 1,000,000 (one million). (Abbreviated M.)
Megawatt-hours: A unit of energy equal to 1,000,000 watt-hours. (Abbreviated MWh.)
Section 2 – BASIC DEFINITIONS – Charge and Current
Charge: Electrical charge, like matter, energy, space, and time, is considered to be a rather fundamental concept, definable only in terms of the effects which it produces which are observed and attributed to the assumed existence of such a thing as “charge”. The postulated existence of “charge” has been found to be useful and workable. If in fact, such a thing as “charge” did exist, it would explain why certain effects were observed. As long as this assumption remains undisputed by evidence to the contrary, we will assume that it is valid.
Here is an example of postulating the existence of something prior to obtaining actual proof of its existence. The planet Pluto (furthest from our sun) was not observed until many years after astronomers first noticed that for some reason, the orbit of the planet Uranus (next to furthest from our sun) was at times aberrated. More observations of orbits were made and more data was gathered. The conclusion drawn from this was that a varying force of unknown origin must have been acting on the planet Uranus. The most logical explanation, the existence of a planet of appropriate size, location, and orbit, was then postulated, and many thousands if not millions of additional man-hours were invested in the subsequent effort to either prove or disprove the postulate. At long last, direct visual confirmation was obtained.
“Charge” is therefore defined in terms of its behavior and its effects on the environment. The following “statements of fact” are the result of intensive scientific investigation and observation and are assumed proven to be accurate. These “facts” are the basis used in order to define charge. Thus far these “facts” have withstood close experimental scrutiny:
1. There are to be 2 kinds of charge. The names given to these are Positive (+) and negative (–).
2. Negative charge (–) is carried by electrons.
3. Positive charge (+) is carried by protons.
4. Electrons and protons carry equal amounts of charge.
5. The quantity of charge carried by each electron or proton is invariable.
6. A proton weighs 1837 times as much as an electron.
7. Charge is an inseparable and always present part or characteristic of all electrons and protons.
8. Charge is neither created nor destroyed. It is conserved.
9. Positive charge is repelled by positive charge. Negative charge is repelled by negative charge. Positive and negative charges are mutually attracted. From this, we obtain the statement “opposites attract and likes repel”.
10. The electrical force of attraction between an electron and a proton, due to the amount of charge each carries, is approximately 1039 times stronger than the gravitational force of attraction between the same electron and proton.
1039 = 10 to the 39th power = 1 followed by 39 zeros
11. Charge, when moved, produces a magnetic field which surrounds the charge being moved. Moving a negative charge would produce a magnetic field equal in strength but exactly opposite in direction to the magnetic field that would be produced by moving an equal amount of positive charge in an identical manner (same speed and same direction).
RIGHT-HAND RULE: The direction of the magnetic field produced by a moving line of positive charge in a straight line would look something like this:
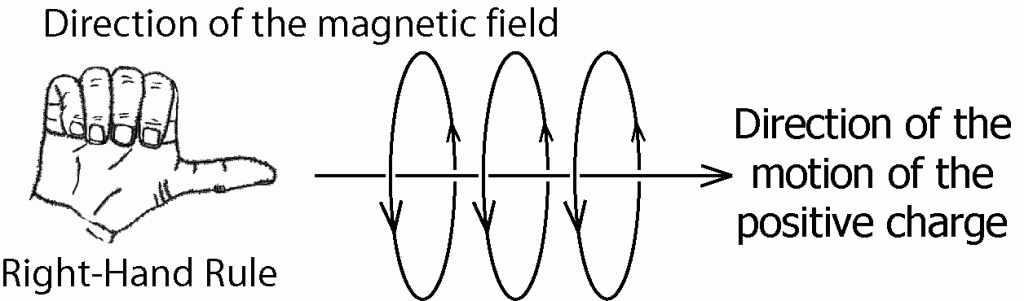
The circles with arrows indicate the direction of the magnetic field about the moving charge, as a compass needle would point if near the moving charge.
12. Charge, when stationary in an unchanging magnetic field, remains unaffected by that magnetic field.
13. Charge, when moved through a magnetic field, crosswise to the direction of the magnetic field, will experience a force directed at right angles to both the direction of that magnetic field and the direction of motion of the charge.
LEFT-HAND RULE: The direction of the force relative to the direction of the magnetic field and the direction of motion of a positive charge can be drawn as follows:

Note 1: Protons exist independently but are most commonly found as part of the nuclei of atoms, where they are tightly bound in by extremely strong forces known as nuclear forces. Electrons are commonly found surrounding atomic nuclei, but are much less tightly bound to the nuclei by the comparatively very weak electrical force of attraction between positively charged nuclei and the negative charge of the electron.
Note 2: A characteristic of some solid materials is that even though the individual atoms of the material may not be free to move about, to various degrees some of the electrons within that material may be free to wander about, moving from atom to atom. These are called FREE ELECTRONS. This phenomenon enables some materials to conduct electricity. The electrons are free to migrate through the material. Materials exhibiting this characteristic are called CONDUCTORS. The best conductors are metals. Materials that do not share electrons from atom to atom in this manner are called INSULATORS.
Note 3: The word “Charge” is commonly used to describe a net excess of either negative or positive charge on or in a body, a volume, a region, or a surface. An example would be the charge that might build up as one walks across a carpet in a dry climate. The buildup may be gradual, but the discharge (static electricity) can be shocking as you reach to grab a doorknob or some other uncharged or grounded object.
Note 4: The word “Charge” also means the action of pumping charge through a device such as a battery so as to increase the device’s ability to flow charge back at a later time.
Electric: Having to do with pushing, moving, storing, using, containing, or otherwise controlling charge. For instance, an electric insulator is used to inhibit the passage of electric charge, whereas a thermal insulator is used to inhibit the passage of heat.
Electricity: Electric charge, the stuff that flows through electric wires and runs motors and lights up light bulbs. This is often used as a catchall word to include any and all phenomena connected with the concept of charge such as the properties of charge, any effects attributed to charge, or the study of charge.
Coulomb: A unit of charge equal to the combined total charge of 6.24 x 1018 electrons.
6.24 x 1018 = 6.24 times 10 to the 18th power = 6,240,000,000,000,000,000
Named in honor of Charles Augustin de Coulomb (1736-1806), a French physicist noted for his extensive research regarding the forces of interaction between charges or charged particles circa 1785. (Abbreviated C.)
The force that would be required to keep 1 coulomb of positive charge separated from 1 coulomb of negative charge, at a distance of 1 mile is approximately 781 pounds. The force necessary to maintain separation at a distance of 100 feet would be 2.2 million pounds.
Additionally, one cubic inch of copper contains approximately 200,000 coulombs of free electrons, approximately 1 free electron per copper atom.
Current: A flow or generalized movement or migration of electrical charge. Current is measured in terms of the amount of charge moving past a specified location in a specific amount of time.
Ampere: A unit of electrical current (rate of flow of charge) equal to 1 coulomb of charge passing or moving by in 1 second of time. (Abbreviated A. or amp.)
Named in honor of Andre-Marie Ampere (1775-1836), a French Mathematician and Physicist, noted for his research into magnetic forces between current carrying conductors circa 1820.
Consider this: What would be the average drift velocity of free electrons through a #12 copper wire, equivalent to a current of one ampere?
Since 1 cubic inch of copper contains approximately 200,000 coulombs of free electrons and a 1 inch length of #12 copper wire (0.08 inches in diameter) has a volume of 0.005 cubic inches, a 1 inch length of #12 copper wire would contain approximately 1,000 coulombs of free electrons.
Thus, in order for 1 coulomb of charge to pass or flow by per second, the free electrons within this conductor must be moving by at an average rate of one thousandth of an inch per second (0.001 inches per second).
Section 3 – BASIC DEFINITIONS – Voltage
Voltage: Electrical pressure which causes or can cause charge to move or flow. Taken from the word Volt.
Volt: A unit of electrical pressure equal to the amount of electrical pressure which if applied and used to push 1 coulomb of charge through some type of load, would result in 1 joule of work being done. (Abbreviated V.)
Named in honor of Alesandro Volta (1745-1827), an Italian scientist noted for his invention of the battery known as the “Voltaic Cell” circa 1800.
How one would compute the amount of work done in pushing some quantity of electric charge from one location to another is quite similar to how one would compute the amount of work done in pumping some quantity of fluid, such as water, from one location to another. For water, the pressure applied times the quantity of fluid moved equals the amount of work done. For electricity, the amount of pressure applied (measured in volts) times the quantity of charge moved (measured in coulombs) equals the amount of work done (measured in joules).
Alternating Current: A term used to refer to any flow of charge which periodically reverses direction in the conducting medium. The term Alternating Current (AC) is used in referring to both currents and voltages of an alternating nature. (Abbreviated ac. or AC.)
Direct Current: A term used to refer to any flow of charge that flows in only one direction in the conducting medium. The current need NOT be steady or constant, as would be the flow from a battery through a light bulb for example. Highly pulsating one directional currents are called direct currents. The term Direct current is used in referring to both currents and voltages of a non-alternating nature. (Abbreviated dc. or DC.)
Section 4 – BASIC DEFINITIONS – Resistance
Resistance: Opposition to the flow of current, a characteristic of the material or device through which the current must flow. Resistance is a property of conductors which are not perfect conductors; the flow of current through the material is to some degree impeded or resisted.
To a greater or lesser degree, all conductors resist the flow of current. An exception to this rule has been found or created under highly controlled laboratory conditions, where perfect conduction (no resistance) has been obtained in certain materials at temperatures near absolute zero. The phenomenon of perfect conduction is known as superconductivity.
Resistor: A device used to provide resistance to the flow of charge. This is generally a manufactured device which provides a specific amount of resistance.
Ohm: A unit of electrical resistance to the flow of charge (an electrical current). One Ohm is the amount of resistance required to limit the flow of current to 1 ampere (1 coulomb of charge per second) when an electrical pressure of 1 volt is applied. (Abbreviated Ω – the Greek letter Omega)
Named in honor of Georg S. Ohm (1789-1854), the German physicist who discovered the relationship of electrical resistance to steady currents and steady voltages circa 1826.
Section 5 – OHM’S LAW
Mr. Ohm researched a large variety of materials and found, for an enormous range of applied steady voltages and currents (DC), that the resistance offered to an electric current by a solid material was independent of either the voltage applied across the material or the current flowing through the material. He found that the amount of current flowing through a resistance increased in proportion to the voltage applied.
Ohm’s Law states that the ratio of the voltage applied across the resistance to the amount of current that then flowed through the resistance is constant. This ratio was found to depend only upon the resistance of the material being tested. As the resistance was increased, the voltage had to be increased in order to force the same amount of current through the resistance.
The unit of resistance, now named ohm, was thus defined to be the amount of resistance that would limit the flow of current to 1 amp when 1 volt of electrical pressure was applied across the resistance.
The following standard notations now need to be introduced:
V = the numerical value of the voltage (in volts) applied across the material.
I = the numerical value of the current (in amps) flowing through the material.
R = the numerical value of the resistance (in ohms) of the material.
V / I = V divided by I, the ratio of voltage (in volts) to current (in amps).
With this defined, the relationship can be written as follows:
V / I = R
This is Ohm’s Law. It can be rewritten in either of the following two equivalent forms:
V = I x R or V / R = I
OHM’S LAW applies to Direct currents and Alternating Currents passing through resistance. Additional factors come into play when Alternating Currents pass through other than a pure resistance. Such factors relating to Alternating Currents will be addressed later.
Section 6 – APPLICATION OF OHM’S LAW
Anytime a resistance has a current flowing through it, a voltage must exist to push that current through the resistance. Ohm’s law gives the magnitude of the voltage necessary to push a specified amount of current through a specific resistance. No current flowing means either no voltage is being applied or the resistance is infinitely large.
As an example of how ohm’s law is applied, consider the following: What voltage would be required to push 5 amps of current through a 24 ohm resistance? This problem can be stated in another way: If 5 amps were known to be flowing through a 24 ohm resistance, what voltage must be being applied?

Ohm’s Law gives the answer:
V = I x R = 5 amps x 24 ohms = 120 volts
Section 7 – CIRCUITS
Circuit: A complete path through which an electric current could flow.
Series Circuit: a circuit in which the entire current which flows through the first element of the circuit, must then flow through the next, and then the next, etc., in sequence. The elements of such a circuit are said to be connected in series. A current which flows through any one element must also flow through each of the other elements.
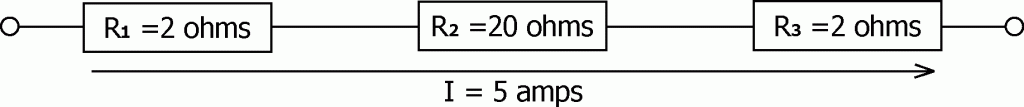
Above is an example of a series circuit. The 3 resistors (R1 = 2 ohms, R2 = 20 ohms, and R3 = 2 ohms) are connected in series. In this example, 5 amps are flowing through the series.
What voltage would need to be applied to each of the 3 individual resistors in order that 5 amps of current would flow through each?
Ohm’s Law states that the voltage (V, in volts) necessary to push a current (I, in amps) through a resistance (R, in ohms) is equal to the product of the current times the resistance. This is written in shorthand as V = I x R. Therefore we have:
V1 = The voltage across R1 = I x R1 = 5 amps x 2 ohms = 10 volts
V2 = The voltage across R2 = I x R2 = 5 amps x 20 ohms = 100 volts
V3 = The voltage across R3 = I x R3 = 5 amps x 2 ohms = 10 volts
What is voltage (V) must be applied across the combination of these 3 resistors connected in series in order that 5 amps flow through the combination?
Rule: The total resistance of a combination of resistances all of which are connected in series, is equal to the sum of the individual resistances.
R = The Total Resistance of the series = R1 + R2 + R3 = 24 ohms
Using Ohm’s law to determine the total voltage (V) which must be applied to the total resistance (R) in order to push the 5 amp current through this series yields:
V = Total Voltage applied to the series = I x R = 5 amps x 24 ohms = 120 volts

Notice that the total voltage across the series of resistors is equal to the sum of the voltages across each of the individual resistors. (Kirchhoff’s second rule.)
Section 8 – VOLTAGE DROP
The voltage drop between any two points in a circuit is the voltage difference between those two points. It is the amount of electrical pressure (measured in volts) required to push the current through that part of the circuit. (In the previous example, the voltage drop across R1 was 10 volts.)
Consider the situation of a hydraulic pump forcing hydraulic fluid out through a short hose out to a hydraulic motor and then back to the pump again through another short hose. Very little energy would be expended or lost in pushing the hydraulic fluid through the two short hoses running between the pump and the motor. The pressure remaining to run the motor would be equal to the pressure from the source, less the combined pressure losses from the two hoses.
If the length of the two hoses were increased, the pressure drop from pushing the hydraulic fluid through these two longer hoses would be increased. As a result, the amount of pressure remaining available to drive the motor would be reduced.
Additionally, The pressure drop due to pumping the fluid through the two hoses, does not depend upon the sequence in which the pump, motor, and hoses are connected, only the combined length of the hoses.
In the previous example showing 120 volts pushing 5 amps through a series of three resistors (2, 20, and 2 ohms), the voltage arriving at the 20 ohm resistance was reduced by 20 volts. That voltage drop was the voltage required to push the 5 amp current through both of the 2 ohm resistors which were in series with the 20 ohm resistor.
The electrical pressure loss from pumping the 5 amp current through the two 2 ohm resistors does not depend upon the sequence in which the resistances are connected. The loss remains the same. This loss of electrical pressure due to energy being expended in pushing current through a resistance of some sort is called VOLTAGE DROP. The voltage drops shown in our example were:
V1 = 10 volts = the voltage drop across R1,
V2 = 100 volts = the voltage drop across R2, and
V3 = 10 volts = the voltage drop across R3.
Copper and Aluminum are not perfect conductors. Though not the same, each exhibits a degree of resistance to the flow of electricity. (Aluminum provides about 63% more resistance per foot of wire than copper.) The resistance (in ohms per thousand feet) for various sizes of both Cu (Copper) and Al (Aluminum) wires can be found in the National Electrical Code (the NEC). Conductor sizes for the smaller wires are given in terms of “AWG” numbers (American Wire Gauge). According to Chapter 9, Table 8 of the NEC, AWG 12 Copper wire has diameter of 0.081 inches and a resistance of 1.93 ohm/M ft (ohms per thousand feet).
From this we determine that a 1036 foot length of #12 solid copper wire will have a resistance of 2 ohms:
0.00193 ohms per foot x 1036 feet = 2 ohms
Thus the example we have been using could be redrawn as equivalent to having the 20 ohm load connected to the 120 volt source by two #12 solid copper wires, each 1036 feet long.

The combined voltage drop of the two wires connecting the load to the supply of voltage is referred to as the voltage drop of the supply conductors. In this example, the total supply line voltage drop is 20 volts = V1 + V3. A 20 volt supply line drop with a 120 volt supply voltage is a 17% voltage drop. This is quite excessive and means that 17% of the power being supplied to the circuit is just being wasted.
Section 9 – POWER
From the definition of volt we have “One joule of work or energy is required to push 1 coulomb of charge through a potential difference or voltage drop of 1 volt.”
The amount of WORK or ENERGY (in joules) required to push or move some amount of charge (Q) through some voltage difference (V) is equal to the product of the amount of charge moved times the voltage difference through which the charge was moved.
WORK DONE = The amount of charge moved from point A to point B times the voltage difference between point A and point B
= Q x V
POWER = The Rate at which Work is being done
= The Rate at which charge is being moved from point A to point B times the voltage difference between point A and point B.
= The current times the voltage difference through which the current flowed
= I x V
POWER and ENERGY are commonly misused words. The unit of power is the watt (joules per second). Watts, kilowatts, megawatts, etc. are units of power (energy per unit of time). Watt-hours, kilowatt-hours, megawatt-hours, etc. are units of energy.
A voltage source by itself is often referred to as a source of power. That is because a voltage source is capable of delivering power (energy at some rate).
The question “What type of power is being supplied?” is really asking questions such as:
Is it AC? Is it DC? What voltage is it? Etc.
The energy one pays the electric company for each month is measured in thousands of watt-hours (kilowatt-hours). If every second, 1 coulomb of charge is pushed through this 1 volt load, then 1 joule of work is being done every second. This is the RATE at which energy is being delivered, 1 joule per second = 1 watt. This is power. The longer this is allowed to continue, the more energy will be delivered. If allowed to continue for one hour then the energy delivered would be = 1 watt-hour. This is energy.
1 watt-hour = 3600 watt-seconds = 3600 joules
Power = V x I = Voltage times the Current = VI
(the x is commonly not printed)
P = Power = the rate of energy transfer in watts,
V = Voltage = the potential difference in volts, and
I = Current = the rate of charge transfer in amps.
As an example of power consumption in a circuit, consider our previous drawing of a 20 ohm load, connected to a 120 volt source by 2 #12 copper wires, each 1036 feet long.

The power used or consumed in the top wire leading to the 20 ohm load is P1.
P1 = V1 x I = 10 volts x 5 amps = 50 watts.
The power used or consumed in the 20 ohm load is P2.
P2 = V2 x I = 100 volts x 5 amps = 500 watts.
The power used or consumed in the bottom wire leading to the 20 ohm load is P3.
P3 = V3 x I = 10 volts x 5 amps = 50 watts.
The total power that is being supplied to the system is P.
P = V x I = 120 volts x 5 amps = 600 watts = P1 + P2 + P3
To some degree, each part of the circuit is a part of the total load supplied by the power source. In this example, the total load consists of the 2 supply lines and what is being called the actual or intended load. Because the supply lines do consume power they are in fact, part of the total load of the circuit.
An example of a resistive load would be the heating element in an electric heater. The fan motor of an electric heater is not purely a resistive load and other effects come into play. For this reason, the study of electrical basics starts with and is at first limited to gaining an understanding of voltages and currents, in relationship to resistive loads. Once this basic study is completed, the more complex relationships between DC and AC voltages and currents, and non-resistive loads can be taken up.
No energy coming into the system is lost. All of it is delivered to the various loads of the circuit and converted into whatever form of energy it is converted into at those individual loads. If the load is a resistance the energy is converted into thermal energy (heat). If the load is a motor, the energy is converted into a combination of mechanical energy (rotation), vibrational energy, and thermal energy (heat). If the load were a storage battery, the energy would be converted into chemically stored potential energy and thermal energy.
The rate at which energy is pumped into the circuit is equal to the sum of the rates at which it is consumed or changed to other forms in all parts of the circuit. The power input is equal to the sum of the power inputs to each of the connected loads which is equal to the sum of the energy output rates plus the energy storage rates of each of the connected loads.
This can be stated briefly as:
ENERGY INFLOWED = ENERGY OUTFLOWED + ENERGY STORED
or
RATE OF INFLOW = RATE OF OUTFLOW + RATE OF STORAGE
The concept of INPUT = OUTPUT + STORAGE applies exactly and can be displayed graphically in the case of the example we are using. In this example, no storage is occurring so the concept reduces to INPUT = OUTPUT, as is drawn below.
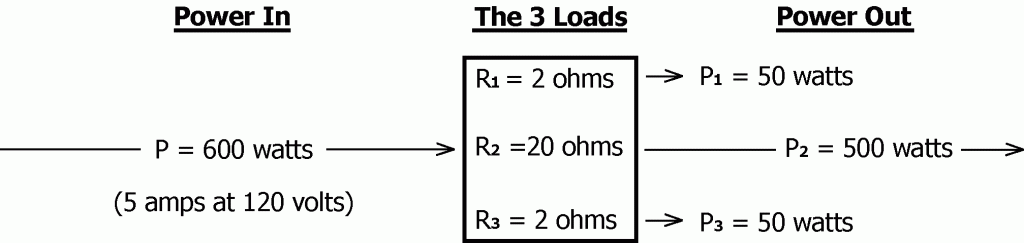
As we have seen above, the power (P) being delivered to a load is equal to the voltage (V) being applied to the load times the current (I) flowing through the load.
P = V x I or P = VI
Ohm’s law states that the voltage (V) applied to the load is equal to the current (I) flowing through the load times the resistance (R) of the load.
V = I x R or V = IR
These two relationships may be combined in two ways that are useful.
Substituting V = I x R into the formula for power yields the following:
Power = P = V x I =I x R x I = I2 x R = I2R (pronounced I squared R)
(The x is commonly not printed nor spoken, so I2 x R becomes I2R)
Substituting I = V / R into the formula for power yields
Power = P = V x I = V x V / R = V2 / R (V squared divided by R)
The formula P = I2R (I squared R) is generally the most useful and commonly seen of the two. With it, one need only know the resistance of the load and the current flowing through the load to calculate the power being delivered to the load.
Using this relationship, the power dissipated in R1, R2, R3, and in the combined total can again be calculated.
P1 = I2R1 = (5 amps)2 x 2 ohms = 50 watts.
P2 = I2R2 = (5 amps)2 x 20 ohms = 500 watts.
P3 = I2R3 = (5 amps)2 x 2 ohms = 50 watts.
P = I2R = (5 amps)2 x 24 ohms = 600 watts.
Notice again that a total of 100 watts of power is being lost in the 2 wires leading to the load. It is lost in the form of heat generated in the wires. 600 watts of power had to be supplied in order that 500 watts arrive at the load. Nearly 17% of the power from the source was lost. Increasing the size of the supply conductors is usually the solution for reducing line losses to a few percent of the total load, an acceptable level.
Section 10 – CHARGING A BATTERY
The action of a 1 volt battery forcing 1 coulomb of charge to flow through some load. This would require that 1 joule of work be done by the battery.
The action of forcing charge to flow back into the battery in the opposite direction to the push being exerted by the battery would require that work be done on the battery.
The first way, the battery is doing the work, and the second way, the battery is receiving work done by an external source. The source could be a generator, a battery charger, another battery, or some other means forcing charge to flow back into the battery.
It is only necessary that the voltage of the external source be greater than the voltage of the battery receiving the charge. Then charge will flow from the external source back into the battery. The greater the voltage of the external source, the faster charge will flow from the external source back into the battery. Too much voltage and could cause the battery to explode.
Section 11 – POWER LOSS
Power loss due to heating in the wires delivering power to a load is commonly called “line loss,” “I squared R heating,” “I squared R loss,” or “Joule heating.”
Minimizing power loss due to heating in the conductors delivering power to the intended loads is of great interest to power companies. The amount of power loss due to the resistance of the millions of miles of power transmission lines owned by the power companies could dissipate so much energy that it would be impractical or too costly to provide electricity on a widespread basis.
If the size of the conductors bringing the power from the generating station to the customer could be increased so that the resistance of the wires was reduced, this would reduce line loss. As an example, 100 miles of #12 copper wire has a resistance of approximately 1000 ohms:
R = 100 miles x 5280 ft/mile x .00193 ohms/ft = 1019.04 ohms
If the wire size were increased to the equivalent of 10,000 #12 wires, the resistance would be about 0.1 ohms per 100 miles and the diameter of the wire would be about 8.1 inches. Though this is a bit larger than any size commonly used for power transmission, it will be adequate for this discussion.
If this 8.1 inch diameter wire were used to supply 100,000 amps of current at 120 volts to a small city at the 100 mile distance, the combined voltage drop in the 2 wires feeding the city would be:
V2LINES = IR = 100,000 amps x .1 ohm x 2 lengths of wire = 20,000 volts.
The voltage at the generating station would therefore need to be 20,120 volts =20,000 volts combined line drop plus the 120 volts for the load.
The amount of power delivered to the city would be:
PCITY = IV = 100,000 amps x 120 volts
= 12,000,000 watts = 12 megawatts.
The line loss (the amount of power lost due to heating in the conductors feeding the city) is calculated to be:
P2LINES = IV = 100,000 amps x 20,000 volts
= 2,000,000,000 watts = 2,000 megawatts
The line drop could also have been calculated using the formula P = I2R,
P2LINES = I2R = (100,000 amps)2 x .2 ohms
= 2,000,000,000 watts = 2,000 megawatts.
The generating station must produce 2,012 megawatts of power in order to deliver 12 megawatts to the city. Nonetheless, increasing the wire size did reduce the line loss.
When electricity generation and transmission was in its infancy, transmission power loss was the problem. Line losses could easily eat up far more power than could be delivered to the city. But the solution was found. And without at this point going into all of the exact details of how it was done, we will now look at the solution:
If the output voltage of the generating station were transformed to a higher voltage, then less current would need be pushed through the wires leading to the city in order to deliver the required 12 megawatts of power to the city. With less current needing to be pushed through the wires to the city, the line loss would be reduced. Then, by reducing the voltage back to desired voltage the problem could be solved. This was the deciding factor as to why AC power was chosen over DC power for long distance power transmission. AC power could easily and economically be transformed to higher or lower voltages using devices called transformers. DC could not.
To demonstrate how this might work, we will assume that the city still needs 100,000 amps at 120 volts. Assume also that the voltage output of the generating station has been transformed up to 12,000 volts. Then the 12 megawatts needed to run the city could be provided by the Power Company if only 1,000 amps at 12,000 volts were delivered through the supply lines to the city.
The line loss would thus be reduced to:
P2LINES = I2R = (1000 amps)2 x .2 ohms
= 200,000 watts = 0.2 megawatts
Thus the generating station would have to produce a total of 12.2 megawatts of power in order to deliver 12 megawatts to the city. This represents approximately a 1.6% line loss, with 98.4% of the power produced at the generating station surviving the trip to be sold to the customer.
The voltage drop in the lines delivering power to the city is:
V2LINES = IR = 1,000 amps x .2 ohms = 200 volts
The amount of power delivered to the city would be:
PCITY = IV = 1000 amps x 12,000 volts
= 12,000,000 watts = 12 megawatts.
At the city, the power would then be transformed back to 120 volts and used. This is approximately how it could be done. In actual fact, the power is be transformed back to whatever voltage is needed. Depending on the size and shape of the city, the power would be brought down to a lower voltage at various locations about the city. Then it is distributed to other more numerous locations where it is again be transformed to even lower voltages, eventually to whatever voltage is needed by the customer.
Transformers are quite efficient devices. They dissipate or loose only a very small fraction of the total power which passes through and is transformed. They are also quite inexpensive to build and maintain compared to the cost of the power that would otherwise be lost and the cost of the extremely large wires that at low voltages would be needed for efficient transmission of electrical power.
Power transmission losses are thus reduced by a combination of voltage transformation and conductor size increase. The extent of either is determined by cost and need. Every business must make a profit if it is to survive. Larger wire and higher voltages increase construction and maintenance costs. Smaller wires and lower voltages increase costs due to line loss. Power transmission and distribution systems are designed to get the job done efficiently, effectively, economically and profitably.
Section 12 – EFFICIENCY
EFFICIENCY: The ratio of usable output power to total input power.

EFFICIENCY = USABLE OUTPUT POWER divided by TOTAL POWER INPUT
EFFICIENCY = POUT / PIN
USABLE OUTPUT POWER = TOTAL POWER INPUT times the EFFICIENCY
POUT = PIN x EFFICIENCY
Electric motors are not 100% efficient. The output of a 1 horsepower motor should be 746 watts. (By definition, 1 hp = 745.6 watts.) If the efficiency of the motor were 75%, then the electrical power input needed in order to fully power the electric motor would be:
Motor Input Power = Motor Output Power / Efficiency = = 746 watts /0.75 = 995 watts.
Let’s look at the efficiency of a complete system, step by step from generation, through transmission, to utilization. (All numbers have been rounded off.)
If the motor were connected to the power source in such a way that 5% of the electrical power fed into the power transmission lines was lost, then the efficiency of the power transmission line would be 95%. Therefore the required electrical power input to the transmission line in order to fully power the electric motor would be:
Line Input = Line Output / Efficiency = 995 watts / 0.95 = 1,047 watts.
If the power source were a gas engine driven generator, with a generator efficiency of 80%, then the required mechanical power input to the generator in order to fully power the electric motor would be:
Generator Input = Generator Output / Efficiency = 1,047 watts / 0.80 = 1,309 watts.
If the gas engine had an efficiency of 35%, then the required chemical power input to the gas engine in order to fully power the electric motor would be:
Engine Input = Engine Output / Efficiency = 1,309 watts / 0.35 = 3,740 watts.
The total efficiency of such a system is simply the product of all of the individual efficiencies:
Total Efficiency = ETOTAL = EMOTOR x ELINE x EGENERATOR x EENGIN = 19.95%
( 0.75 x 0.95 x 0.80 x 0.35 = 0.1995 )
POUT = PIN x EFFICIENCY = 3740 watts x 0.1995 = 746 watts
Thus it can be seen that 3,740 watts (approximately 5 horsepower) of chemical input power (gasoline) would be required to fully power the 1 horsepower electric motor, yielding 746 watts of mechanical output power.
The missing 4 horsepower was converted to other energy forms: heat, vibration, and noise mostly. It can all be accounted for, but only 1 horsepower (20%) made it all the way to whatever machine the motor was used to drive. Nevertheless, if the machine owner profits adequately from the machine’s production, then he will probably continue using that machine.
Section 13 – TEMPERATURE AND RESISTANCE
The resistance of most solid conductors increases as the temperature of the conductor increases. The resistance of Copper increases 0.22 % per degree Fahrenheit of temperature rise at or near room temperature. The resistance of Tungsten increases 0.25 % per degree Fahrenheit of temperature rise at or near room temperature. The resistance of Carbon decreases 0.03 % per degree Fahrenheit of temperature rise at or near room temperature.
Tungsten is mentioned because it and alloys of Tungsten are commonly used as the heat producing resistance element in both light bulbs and heaters.
The common light bulb is useful as an excellent example of how resistance changes with temperature. Using a cheap ohmmeter, the resistance of a 200 watt, 130 volt, Tungsten filament lamp I found in the back of the shop measured 6.1 ohms at room temperature. The voltage available measured 120 volts. When energized, the current flowing through the lamp measured 1.4 amps.
If the resistance of the lamp filament did not change when its temperature increased, then the current through the lamp would be:
I = V / R = 120 volts / 6.1 ohms = 19.7 amps.
That would be equivalent to 2364 watts = 120 volts x 19.7 amps. But the current was measured to be 1.4 amps. Ohm’s law reveals that the resistance of the light bulb’s filament must have increased by a factor of about 14:
R = V / I = 120 volts / 1.4 amps = 85.7 ohms.
Additionally, the actual power output of the lamp was:
P = I x V = 1.4 amps x 120 volts = 168 watts.
If the lamp was rated 200 watts, why was the power output only 168 watts? This because the lamp was rated 200 watts at 130 volts. This is not to say that the power output would have been exactly 200 watts at 130 volts, but it would have been closer.
Using 130 volt rated lamps in place of 120 volt lamps results in much longer lamp life, at least several times the normal life expectancy of a 120 volt lamp. As the voltage is reduced from 130 volts to 120 volts, the light output is reduced slightly and the color shifts toward red a bit.
Section 14 – PARALLEL CIRCUITS
In Parallel: The elements of a circuit are said to be connected in parallel when each of the elements is directly connected to the same supply line.
Below is an example of a parallel circuit. Two resistance loads (R1 = 20 ohms and R2 = 16 ohms) are connected in parallel. For this example I have made the lengths of the supply lines short and of negligible resistance.

The total current being supplied to the two resistance loads connected in parallel is equal to the sum of the individual currents flowing through the two loads:
Supply Current = I = I1 + I2 = 16 amps
Since the supply line voltage drop is negligible, the voltage across R1 and R2 is equal to the supply voltage, V = 120 volts. Thus the currents I1 and I2 through resistances R1 and R2 respectively, and the total current I are easily calculated using ohm’s law:
I1 = V / R1 = 120 volts / 20 ohms = 6 amps
I2 = V / R2 = 120 volts / 12 ohms = 10 amps
I = I1 + I2 = 16 amps
The resistance equivalent to the parallel circuit can be calculated using ohm’s law:
R = V / I = 120 volts / 16 amps = 7.5 ohms
Now what if the above parallel circuit were supplied by long lengths of wire for which the resistance was not negligible, similar to some of the earlier examples? How would one analyze such a circuit?
For example, what if the above two resistance loads connected in parallel were now supplied by two #12 Copper conductors, each approximately 103.6 feet long?
The resistance per thousand feet of #12 Copper wire can be found in Table 8 of the National Electrical Code (NEC), approximately 1.93 ohms/kft (ohms per thousand feet), and the supply line resistance computes to be approximately 0.2 ohms per line.
RLINE = 0.2 ohms = .00193 ohms/ft x 103.6 ft
For series connected resistances, the total resistance is equal to the sum of the individual resistances. Thus the combined resistance of two supply lines is 0.4 ohms, and total resistance of the circuit is the sum of the 2 supply line resistances plus the load resistance.
R = 0.2 ohms + 7.5 ohms + 0.2 ohms = 7.9 ohms
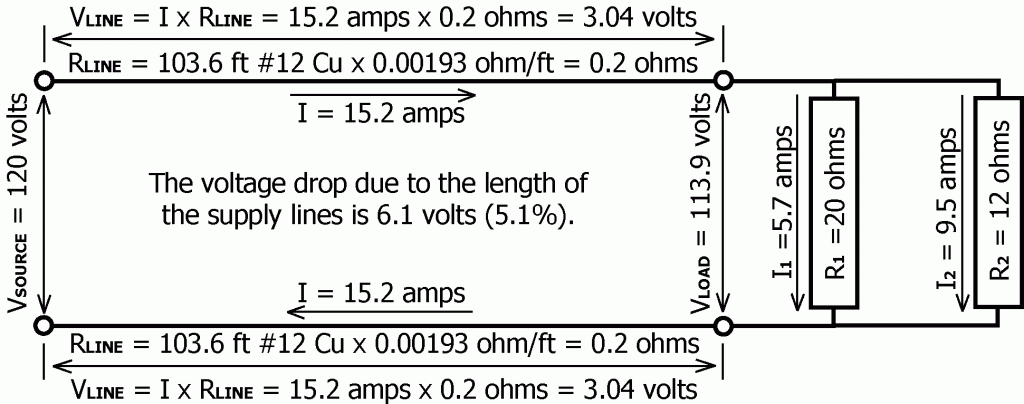
The current flowing through the supply lines to the load can now be calculated:
I = VSOURCE / R = 120 volts / 7.9 ohms = 15.2 amps
And the voltage drop in each of the supply lines can also be calculated:
VLINE = I x RLINE = 15.2 amps x 0.4 ohm = 3.04 volts
Thus the total voltage drop in the supply lines is approximately 6.1 volts, and the voltage applied to the load will be only 113.9 volts (120 volts – 6.1 volts = 113.9 volts). With this established, the current through each of the individual loads can be calculated:
I1 = V1 / R1 – 113.9 volts / 20 ohms = 5.7 amps
I2 = V2 / R2 – 113.9 volts / 12 ohms = 9.5 amps
I = I1 + I2 = 15.2 amps
What is the effective resistance of these 2 loads connected in parallel? According to Ohm’s Law, if 113.9 volts (V) is able to push 15.2 amps (I) through this parallel combination, then the effective resistance must be:
R = V / I = 113.9 volts / 15.2 amps = 7.5 ohms
What is the effective resistance of the entire circuit consisting of the both supply lines connected in series with the 2 resistance loads which are connected in parallel?
R = V / I = 120 volts / 15.2 amps = 7.9 ohms
How much power will the entire circuit (supply lines plus load) consume?
P = IV = 15.2 amps x 120 volts = 1824 watts
How much of this power was converted to heat in the 2 supply lines and thus lost?
Power Loss = 2 x I2RLINE = 2 x (15.2 amps)2 x 0.2 ohm = 92.4 watts
This could also have been calculated using P = IV:
Power Loss = 2 x IVLINE = 2 x 15.2 amps x 3.04 volts = 92.4 watts
Thus in this example, slightly over 5% of the total power being supplied by the source is being lost or dissipated as heat in the conductors carrying power to the load.
( 92.4 watts / 1824 watts ) x 100 = 5.07%
When power is brought to a building, a single set of large wires is used. The Power Company meters the total amount of energy brought into the building through these wires for billing purposes. The power then passes into a distribution panel. From there, it goes out through many different circuits, all connected in parallel to the single power source. These circuits supply power to various locations to supply power to single or multiple loads, all of which are connected in parallel. Seldom are loads ever connected in series.
An example of a series connected load would be the light bulbs in old-fashioned Christmas tree light sets. In a series connected load, if one load failed to conduct then the flow of power to the other loads connected in series would be halted. If one light failed, then all would go dark, unless some bypass system was built in. Such a series connected set of lights might consist of a string of a dozen 10 volt light bulbs connected so that the whole string could be connected to a 120 volt supply
COMMENT:
In the above two examples of a parallel circuit, the component values were chosen so as to maintain simplicity… round numbers, 16 amps because 16 is 80% of 20, and 20 because commonly 20 amps is the maximum current allowed for #12 Copper wire.
In the second example it seemed that including a supply line voltage drop would be instructive. The National Electrical Code (NEC) suggests that a 5% supply line voltage drop should be about the maximum one should allow in any circuit design. With this in mind, the values for supply line length and wire size were chosen to yield approximately that value.
Joe Duncanson
Copyright © 1986,2011 by Joe Duncanson. All Rights Reserved.